Factorising into a Single Bracket: Explanation, Examples and Questions
Factorising single brackets is required as a stand-alone algebraic skill but it can also be used for rearranging formulae and solving algebraic equations. Factorising into a single bracket is the opposite process of expanding a single bracket.
In this article you will learn how to factorise algebraic expressions into a single bracket.
What Does 'Factorising into a Single Bracket' Mean in Mathematics?
Factorising an algebraic expression into a single bracket means to divide every term of an expression by the highest common factor (HCF).
You then rewrite the expression as the product of the highest common factor and a single bracket containing two or more terms.

If that sounds confusing, don’t worry – we’ll show you plenty of examples!
How to Factorise into Single Brackets
In order to factorise into a single bracket, you need to inspect each term of the expression and find its highest common factor (HCF).
- Find the highest common factor of each term in the expression.
- Write this highest common factor outside of a set of brackets.
- Divide the first term of the expression by the HCF. Write this inside of the bracket.
- Divide the second term of the expression by the HCF. Write this inside of the bracket.
- If you have more than two terms, repeat this process.
Factorising Single Bracket Examples
Table Method
Like we did when expanding brackets, we can also use a table to factorise into brackets.
Example 1:
Factorise 14x + 35
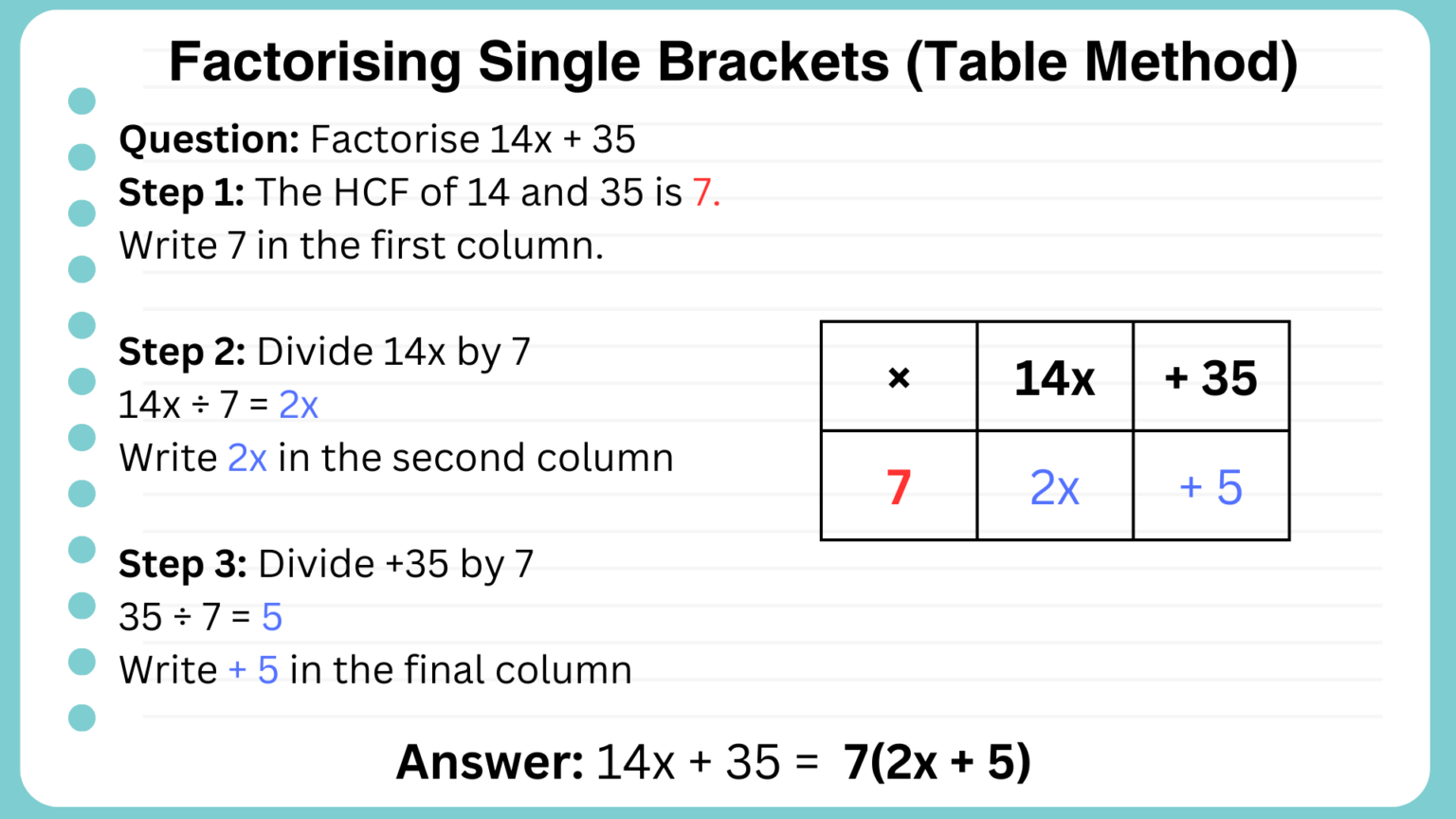
Answer: 7(2x + 5)
Example 2: Including a Negative
Factorise 24x - 16:

Answer: 8(3x - 2)
Factorising with Unknowns in Two or More Terms
If you have variables in more than one of the terms, you also need to find the HCF of the variables.
As an example, let’s consider finding the HCF of \( 9x^2 \) and \( 15x \).
We can find the HCF of the coefficients (the numbers before the variables) and the HCF of the variables separately.
- The HCF of \( 9 \) and \( 15 \) is \( 3 \).
- The HCF of \( x^2 \) and \( x \) is \( x \).
- So the HCF of \( 9x^2 \) and \( 15x \) is \( 3x \).
We use this HCF of \( 3x \) in the example below.
Example 3: Unknowns in Both Terms
Factorise \( 9x^2 - 15x \)

Answer: \( 3x(3x - 5) \)
Inspection Method
As you practise factorising, you’ll learn to do this simply by inspecting and may not need to use a table any more.
Example 1
Question: Factorise \( 4x + 8 \)
Step 1: Find the highest common factor (HCF) of \( 4x \) and \( 8 \).
The HCF of \( 4x \) and \( 8 \) is \( 4 \).
Step 2: Write the HCF outside of the bracket.
\( 4x + 8 = 4(\_ + \_) \)
Step 3: Find the missing values by dividing each term inside the bracket by the HCF.
\( \frac{4x}{4} = x \)
\( \frac{8}{4} = 2 \)
So \( 4x + 8 = 4(x + 2) \)
Answer: \( 4(x + 2) \)
Example 2
Question: Factorise \( 3x^2 - 9x \)
Step 1: Find the HCF of \( 3x^2 \) and \( -9x \).
The HCF of \( 3x^2 \) and \( -9x \) is \( 3x \).
Step 2: Write the HCF outside of the bracket.
\( 3x^2 - 9x = 3x(\_ - \_) \)
Step 3: Find the missing values by dividing each term inside the bracket by \( 3x \).
\( \frac{3x^2}{3x} = x \)
\( \frac{9x}{3x} = 3 \)
So \( 3x^2 - 9x = 3x(x - 3) \)
Answer: \( 3x(x - 3) \)
Example 3
Question: Factorise \( 10x^2 + 8xy \)
Step 1: Find the HCF of \( 10x^2 \) and \( 8xy \).
The HCF of \( 10 \) and \( 8 \) is \( 2 \).
The HCF of \( x^2 \) and \( xy \) is \( x \).
So the HCF of \( 10x^2 \) and \( 8xy \) is \( 2x \).
Step 2: Write \( 2x \) outside of the bracket.
\( 10x^2 + 8xy = 2x(\_ + \_) \)
Step 3: Find the missing values by dividing each term inside the bracket by \( 2x \).
\( \frac{10x^2}{2x} = 5x \)
\( \frac{8xy}{2x} = 4y \)
So \( 10x^2 + 8xy = 2x(5x + 4y) \)
Answer: \( 2x(5x + 4y) \)
Exam Practice Questions
Ready to practise some past paper questions? Choose your syllabus: