Expanding Single Brackets: Explanation, Examples and Questions
Expanding single brackets is a fundamental skill in algebra, useful for rearranging formulae and solving equations. In this guide, we cover how to expand single brackets with step-by-step examples.
What Does ‘Expanding Single Brackets’ Mean?
Expanding single brackets involves multiplying the term outside the bracket by every term inside the bracket.
This process is the opposite of factorising brackets and is key to solving various types of algebraic problems.

Expanding and Factorising Single Brackets
For example, to expand 5(-3x + 7):
- Multiply 5 by -3x to get -15x.
- Multiply 5 by +7 to get +35.
Answer: -15x + 35
How to Expand Single Brackets
- Multiply each term inside the bracket by the term outside the bracket.
- For more than two terms, continue multiplying each one by the outside term, ensuring the correct sign between terms.
Examples Using the Table Method
Example 1: Two Terms
Expand 2(x + 7) by using a table.
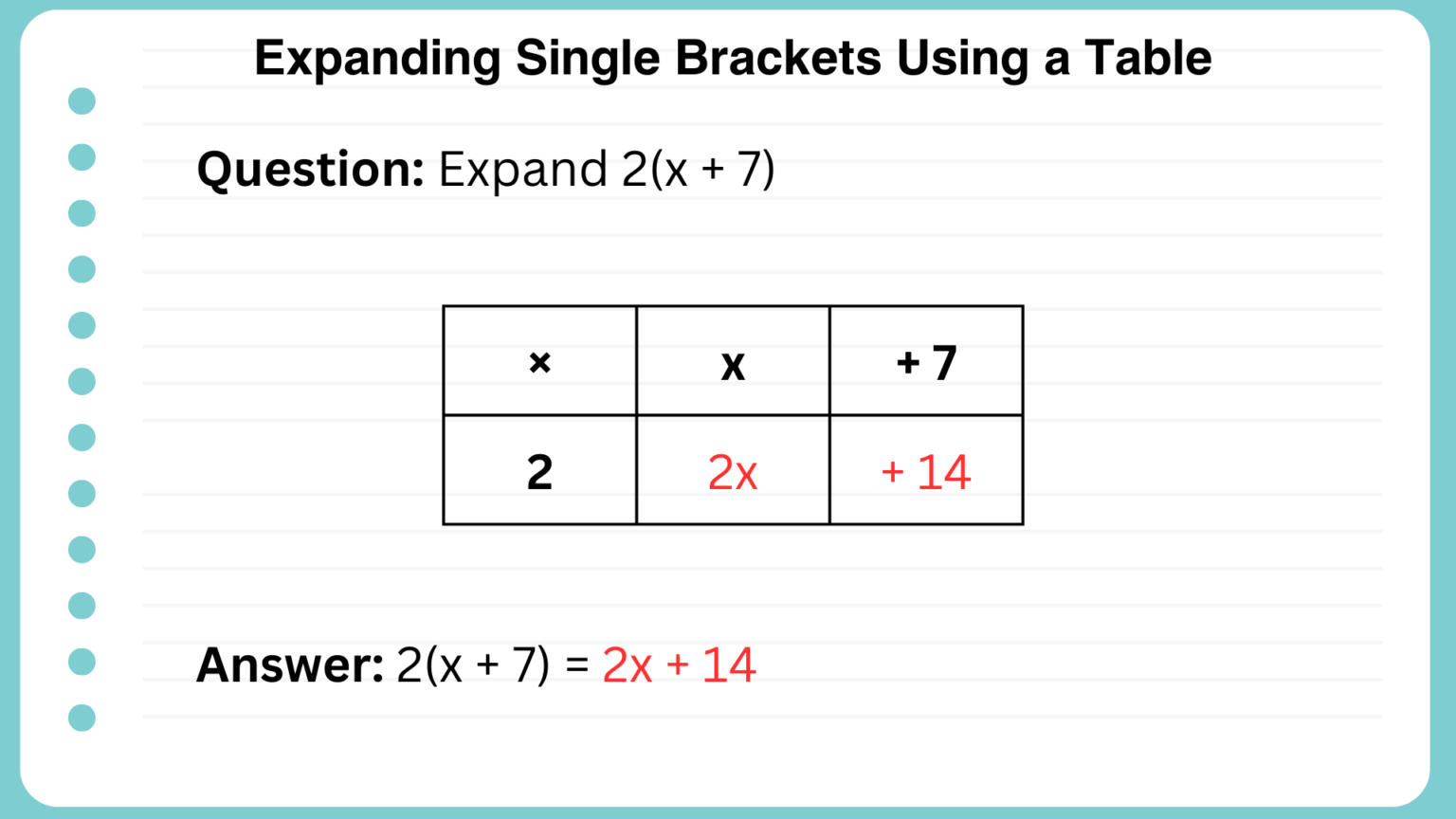
Answer: 2x + 14
Example 2: Two Terms, Including a Negative
Expand 5(2x - 9):
Hint: Don’t forget to include the sign in front of the term.
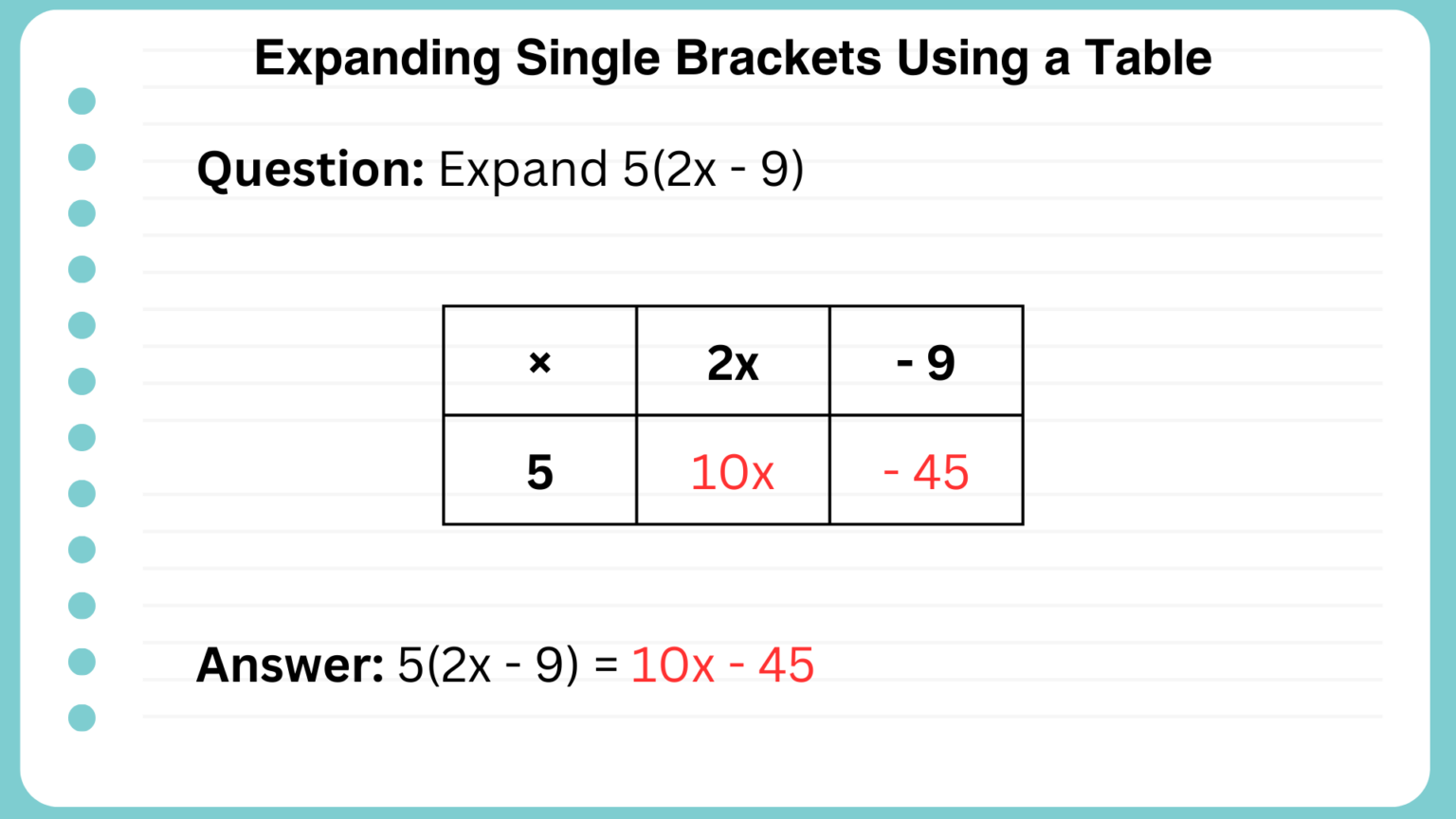
Answer: 10x - 45
Example 3: Two Negative Coefficients
Expand -5(7x - 8):
Hint: If you have a negative sign outside of the bracket don’t forget to include tje negative in the multiplication. In this example we are multiplying by -5 (not 5).
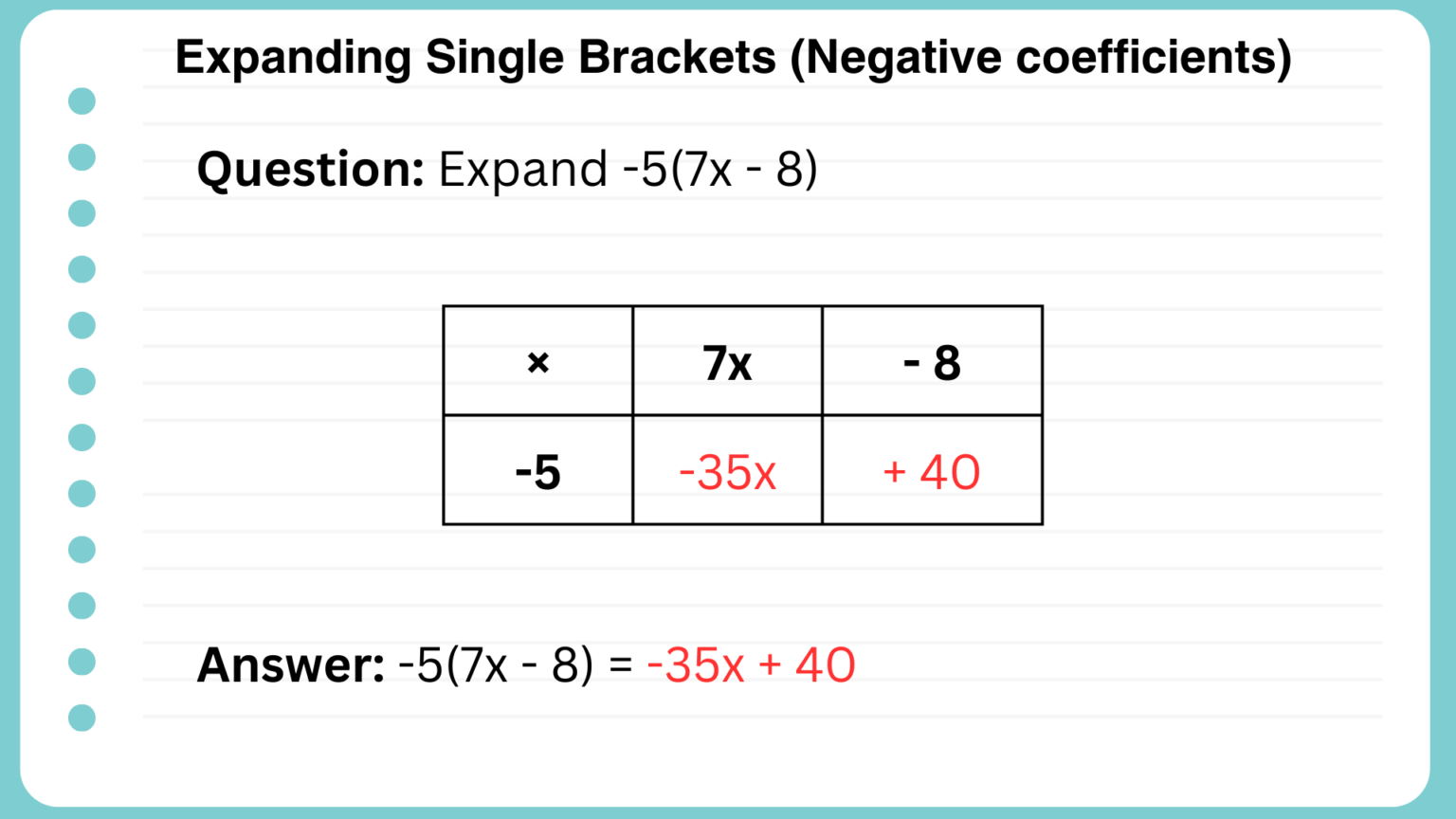
Answer: -35x + 40
Example 4: Expanding with Variables Outside of the Bracket
Expand -7x(4x - 5):
Multiply both the coefficients and the variables.
Hint: remember that \( x \times x = x^2 \). Not \( 2x \)!
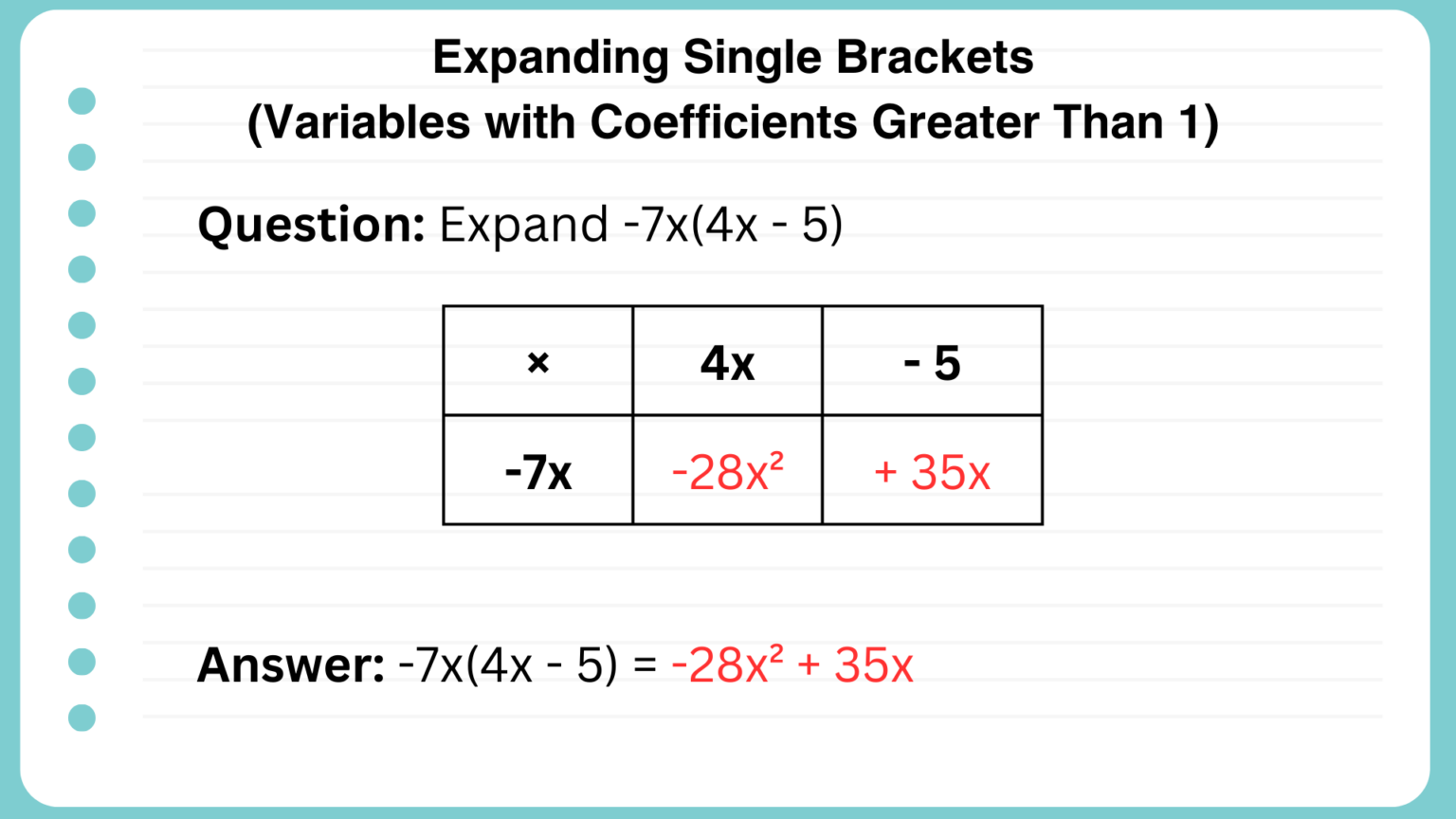
Answer: \( -28x^2 + 35x \)
Example 4: Expanding Single Brackets with Three Terms
Expand 2x(-3x + y - 3):
For a bracket with three terms we need an extra column.
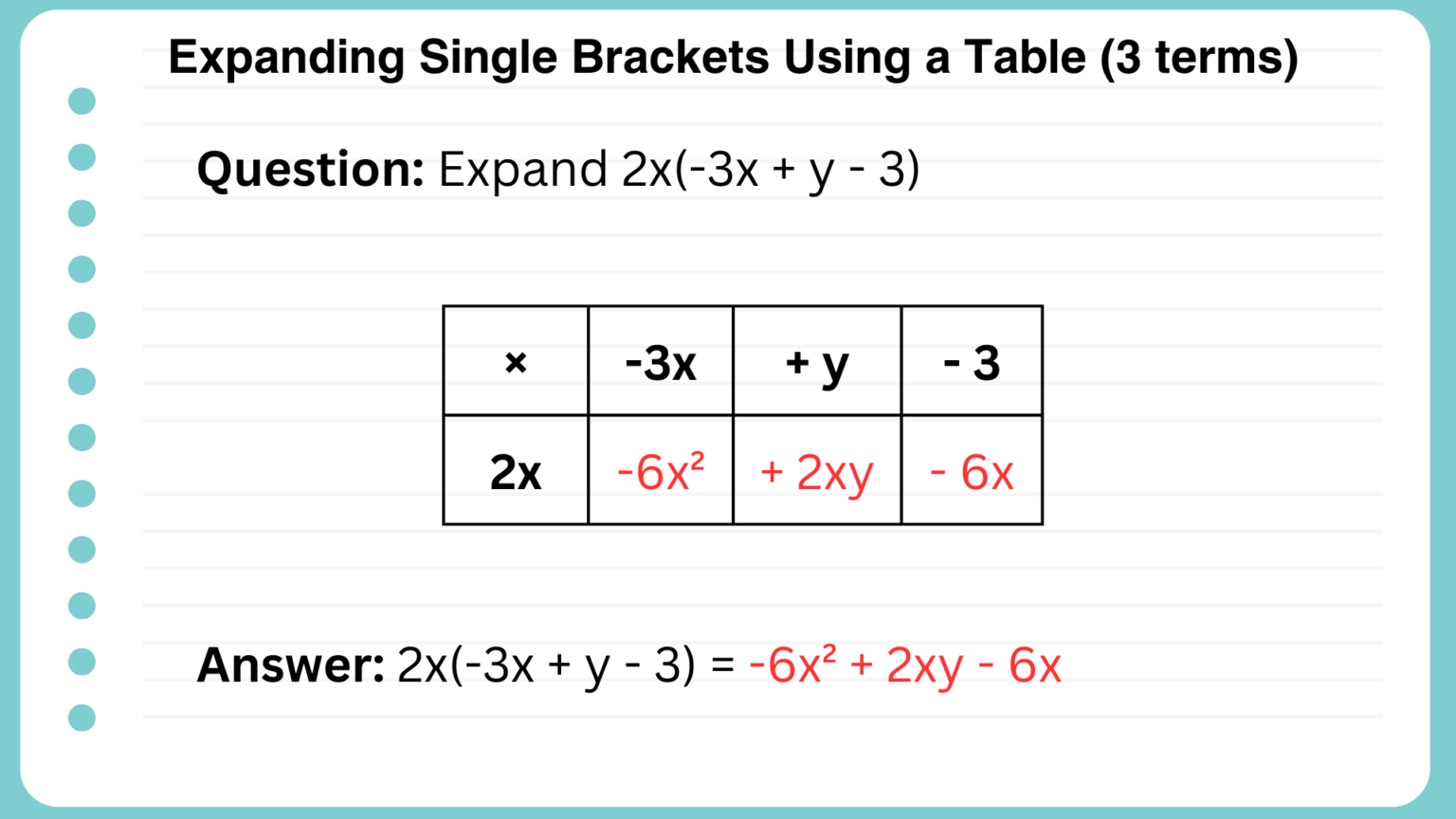
Answer: \( -6x^2 + 2xy - 6x \)
‘Multiplying Out’ Method
Once you become more confident using the table method you may be able to multiply mentally without the need for a table.
The use of arrows can be helpful in demonstrating which terms are being multiplied. The following examples may help to demonstrate.
Hint: If doing this without the use of a table make sure to double check the positive and negatives signs of each term as it is a common mistake to write the wrong sign.
Example 1: Multiplying Out Single Brackets
a) Expand 5(-3x + 7):
b) Expand -3(-8x + 11):

Answer:
a) -15x + 35
b) 24x - 33
Example 2: Multiplying Out Single Brackets (3 terms)
a) Expand \( 7(2x - 9y + 3) \):
b) Expand \( -3x(8x^2 + 10x - 3) \):

Answer:
a) \( 14x - 63y + 21 \)
b) \( -24x^3 - 30x^2 + 9x \)
Exam Practice Questions
Ready to practise some past paper questions? Choose your syllabus:
Expanding Single Brackets Problems
Area Problem
To visualise expanding a single bracket we can imagine a rectangle whose area is calculated by multiplying the length by the width.
We can calculate the total area by adding the two smaller areas (as in method 1).
Alternatively, we can find the total area by multiplying the width by the total length of both rectangles, which is \( 3 \times (x + 7) \). We write this as \( 3(x + 7) \), which then needs to be expanded.
Example 1: Finding the Area by Multiplying Brackets
Find the total area of the larger rectangle.
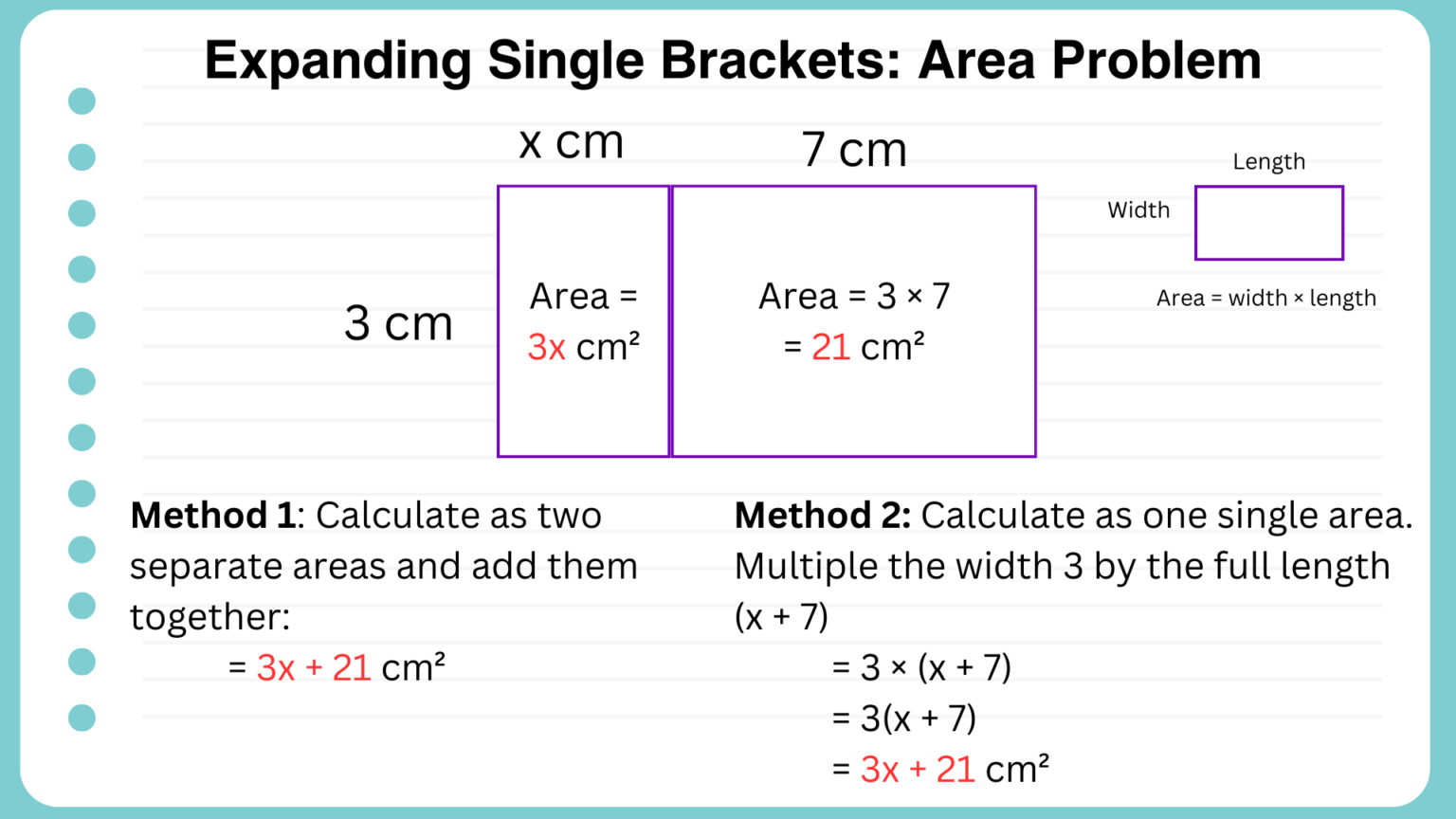
Answer: 3x + 21