Expanding Double Brackets: Explanation, Examples and Questions
Expanding double brackets is an algebraic skill that might seem difficult at first but is actually quite a simple skill. It can be required for use in solving quadratic equations and sketching quadratic graphs.
What Does ‘Expanding Double Brackets’ Mean?
Expanding double brackets means to multiply two brackets together so that every term in the first bracket is multiplied by every term in the second bracket.
For example, (x + 2)(x + 5) means (x + 2) multiplied by (x + 5).
This process is the opposite of factorising quadratics and can be useful in solving various types of algebraic problems.
Here are some examples of expanding double brackets:
\((x + 3)(x + 5) = x^2 + 8x + 15\)
\((y + 2)(y - 9) = y^2 - 7y - 18\)
\((2x + 1)(x - 7) = 2x^2 - 13x - 7\)
In each case, the brackets on the left side of the equation have been expanded (multiplied) and rewritten without brackets on the right side of the equation.
If you’re not sure how this was done, don’t worry! We have plenty of examples.
How to Multiply Two Brackets
Table Method
If you read our guide to expanding single brackets, you might find it easy to use a table to multiply the two brackets together.
Step 1: Write out the first bracket in the top row and the second bracket in the first column of a multiplication table.
Step 2: Complete the multiplication table.
Step 3: Add together every term from the multiplication table.
Step 4: Simplify the expression by collecting like terms (if necessary).
The table method can help to visualise the multiplication. It also helps to avoid making mistakes when negative numbers are introduced.
Example 1: Table Method
Expand \( (x + 5)(x + 8) \) using the table method:
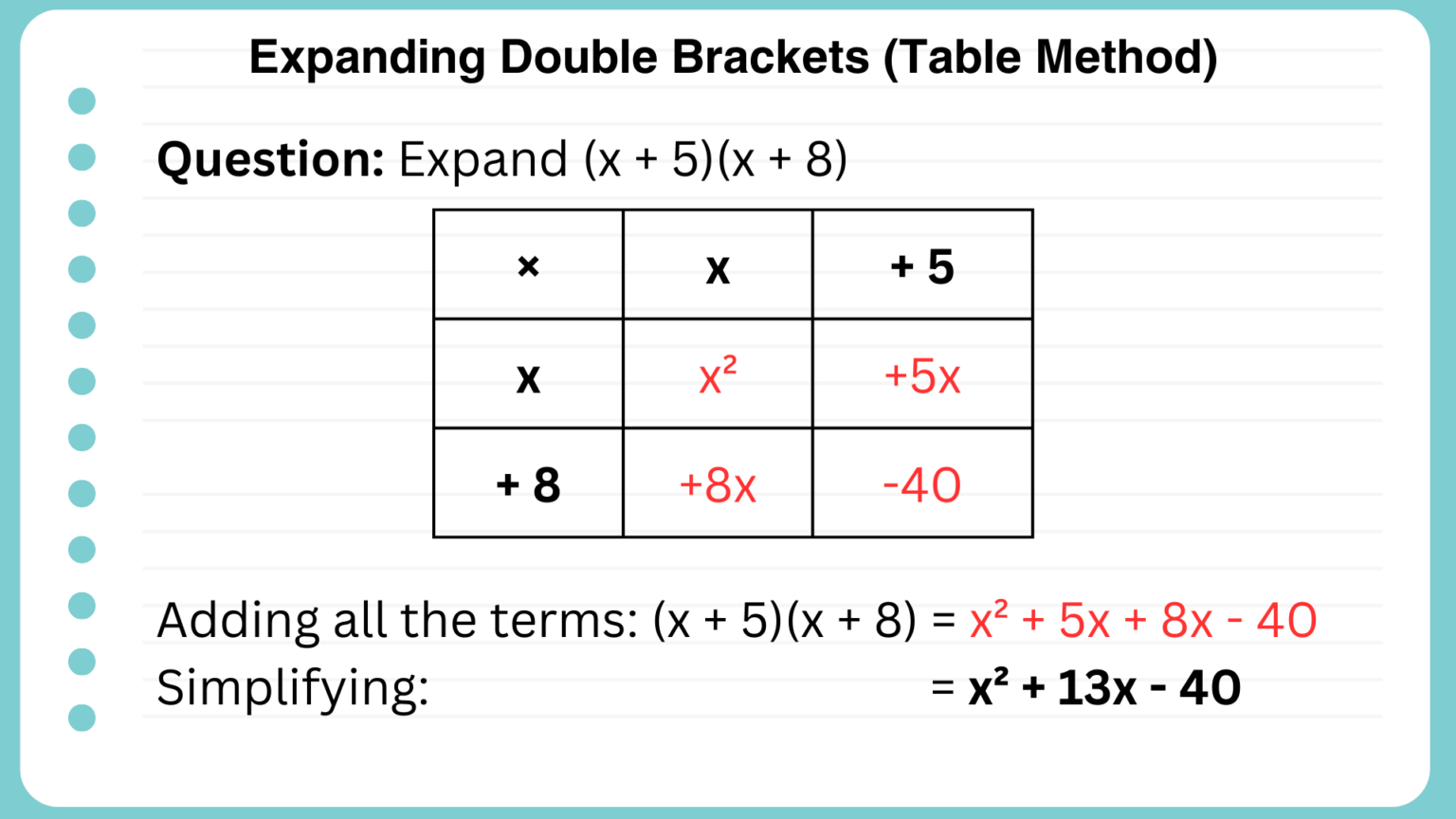
Answer: \( (x + 5)(x + 8) = x^2 + 13x - 40 \)
Example 2: Table Method with Negatives
Hint: If either of the brackets contain negative coefficients, don’t forget to include the negatives in the table.
Expand \( (x - 11)(-x - 3) \) using the table method:
Answer: \( (x - 11)(-x - 3) = -x^2 + 8x + 33 \)
Example 3: Table Method with Coefficients Greater Than 1
If the variables have coefficients greater than 1 (eg. 3x, 7x², 5y), don’t forget to include them in the multiplication table.
Expand \( (3x + 2)(-2x - 5) \) using the table method:
Answer: \( (3x + 2)(-2x - 5) = -6x^2 - 19x - 10 \)
Example 4: Table Method with More Than One Variable
Algebraic expressions with more than one variable can also be multiplied. Remember that for example, 3x × 2y = 6xy and this cannot be simplified any further.
It’s also possible that after adding all the terms together, you won’t have any like terms. If is the this case your answer cannot be simplified.
Expand \( (5x + 2y)(3x - 6) \) using the table method:
Answer: \( (5x + 2y)(3x - 6) = 15x^2 + 6xy - 30x - 12y \)
By Inspection (FOIL Method)
If you feel comfortable with the table method, then you may want to try multiplying brackets without a table. One way to do this is by drawing arrows from each term in the first bracket to each term in the second bracket to make sure you complete all four parts of the multiplication.
This is sometimes referred to as the FOIL method: First, Outer, Inner, and Last.
- Multiply the first terms of both brackets together.
- Multiply the outer terms of the brackets (the first term of the first bracket by the last term of the second bracket).
- Multiply the inner terms of both brackets (the second term of the first bracket by the first term of the second bracket).
- Multiply the last terms of both brackets together.
- Add together all of the terms and simplify.
If the instructions sound confusing, don’t worry—it’s clearer in the examples below.
Example 1: FOIL Method
Expand \( (x + 5)(x - 2) \)
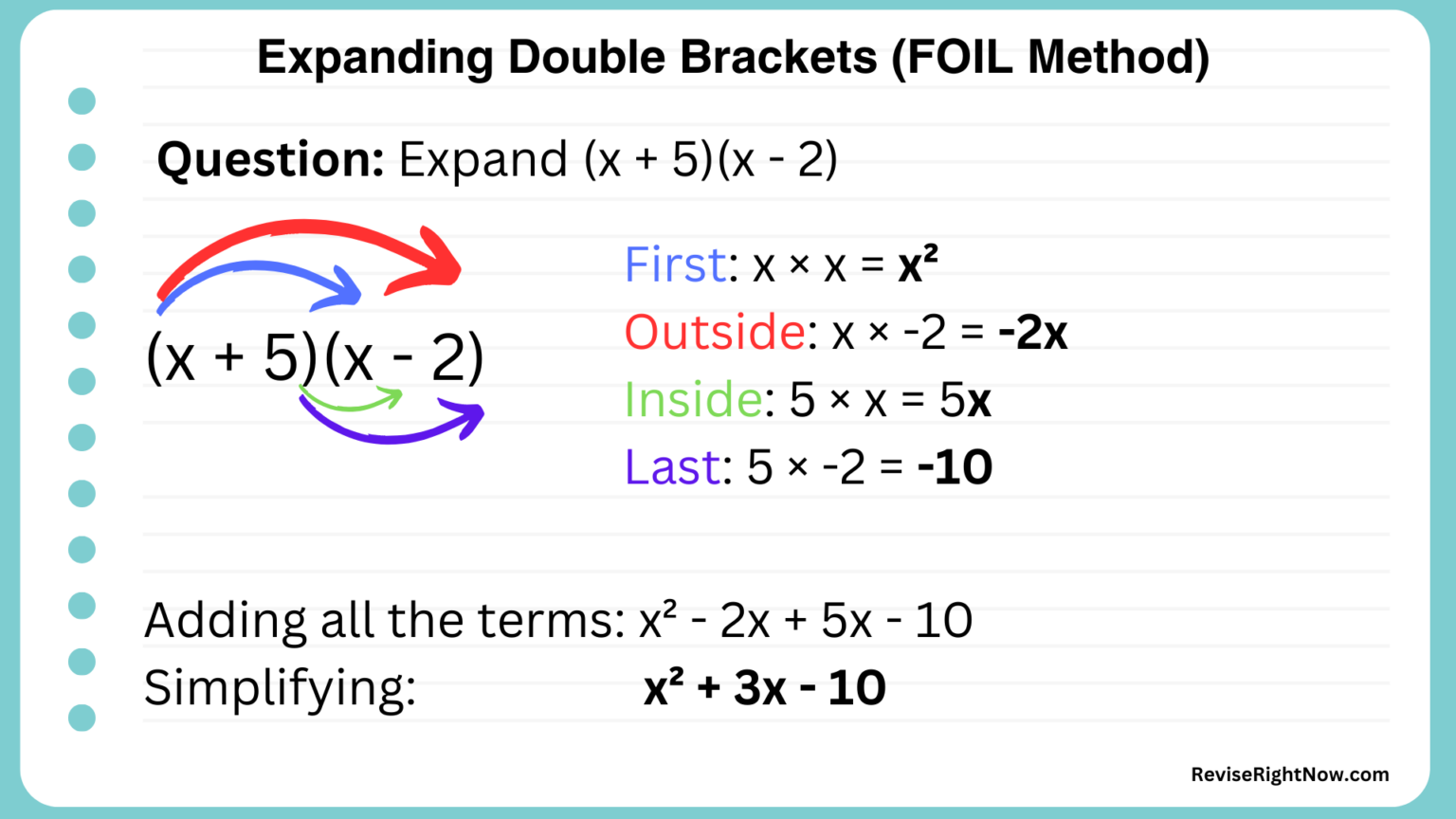
Answer: \( (x + 5)(x - 2) = x^2 + 3x - 10 \)
Example 2: FOIL Method
Expand \( (2x + 3)(x - 7) \)
Answer: \( (2x + 3)(x - 7) = 2x^2 - 11x - 21 \)
Now you know how to expand brackets, try multiplying brackets including surds.