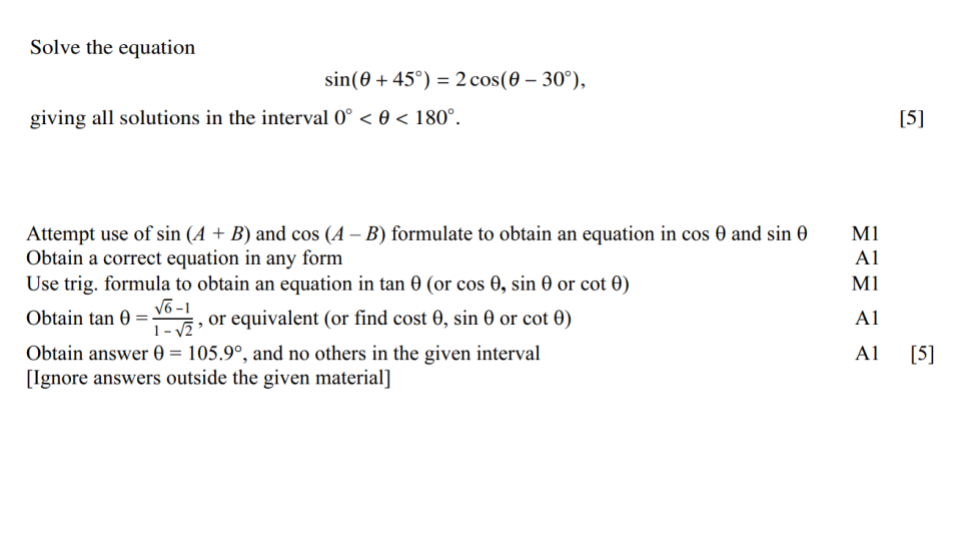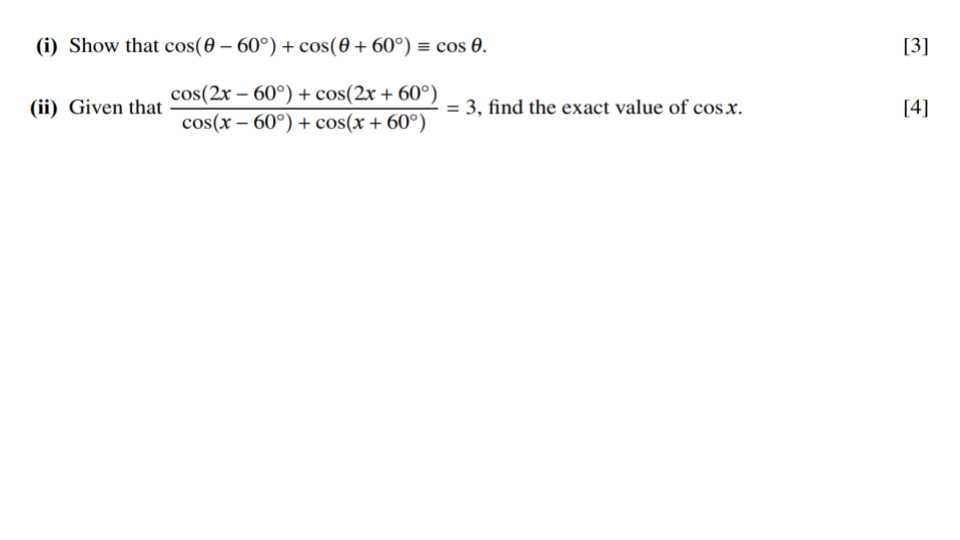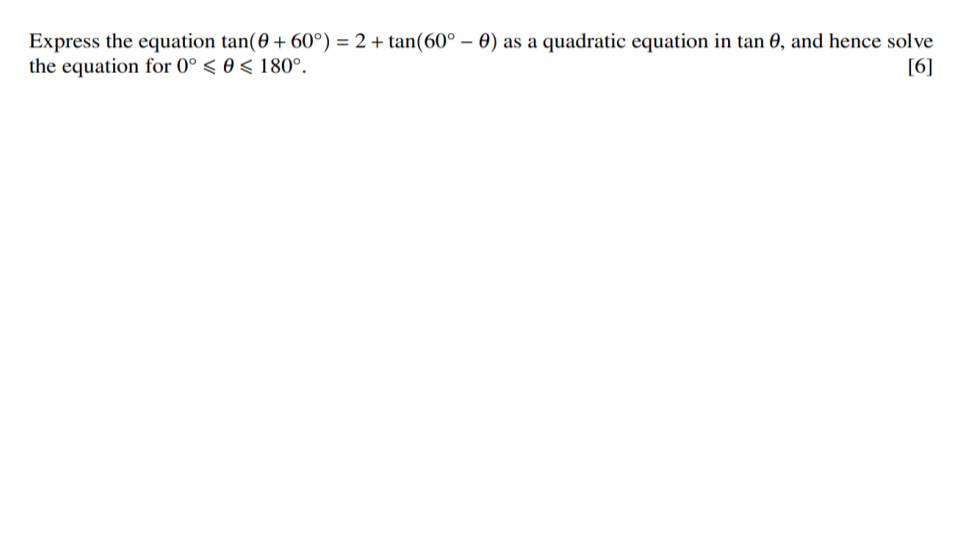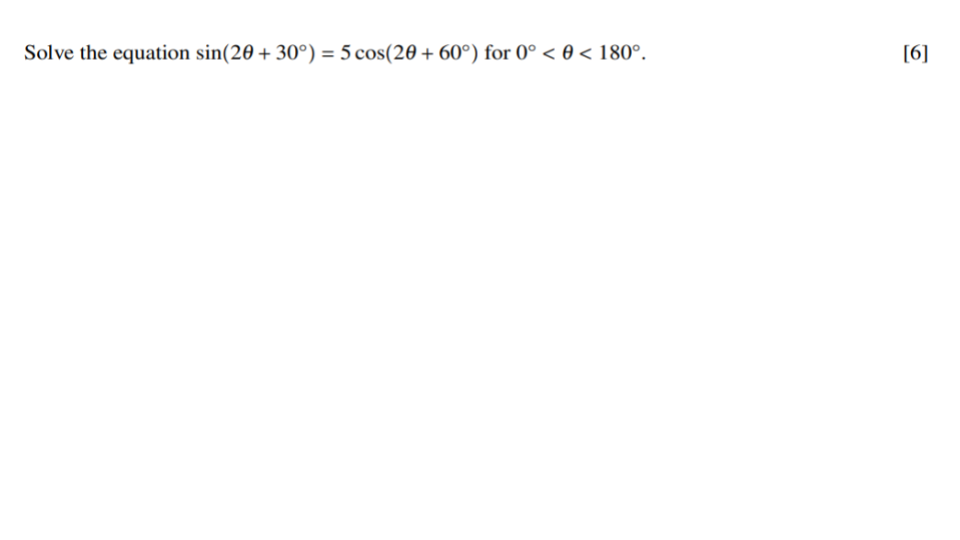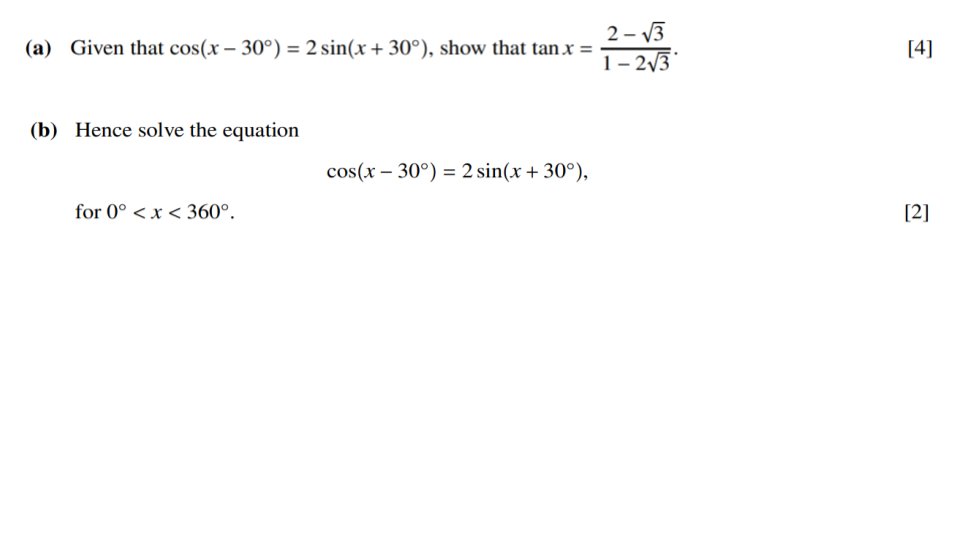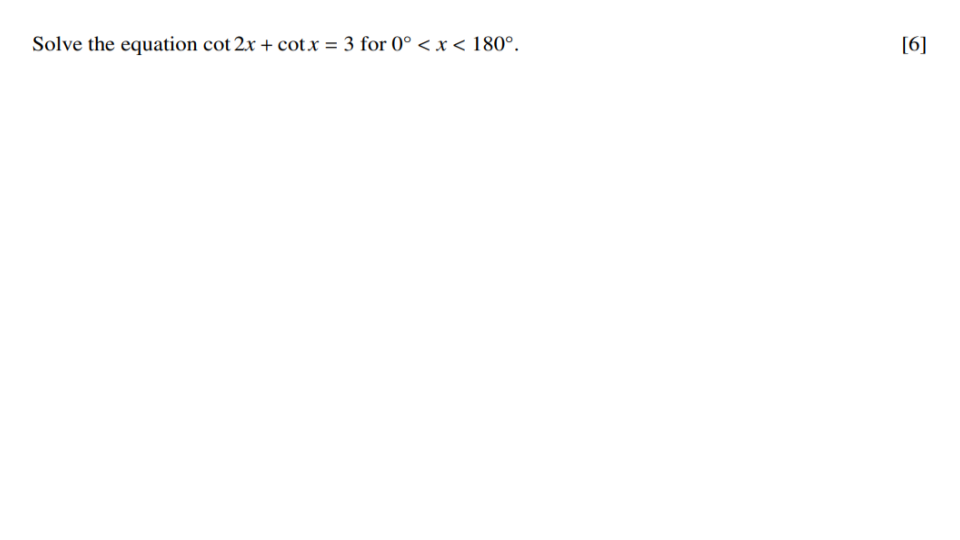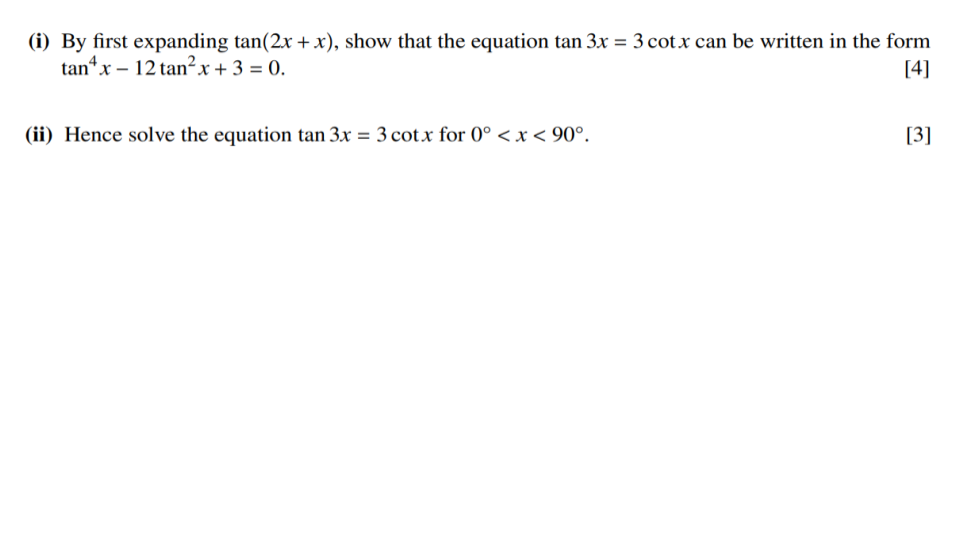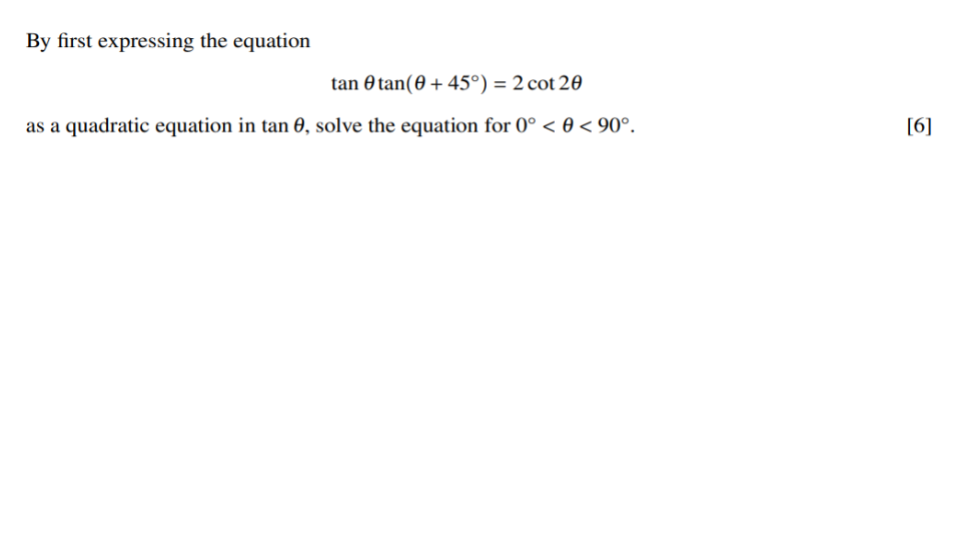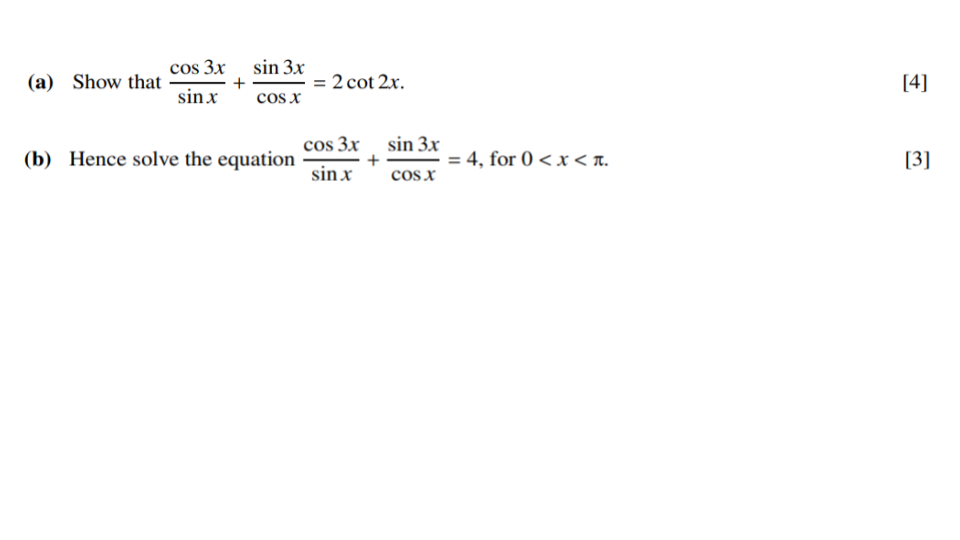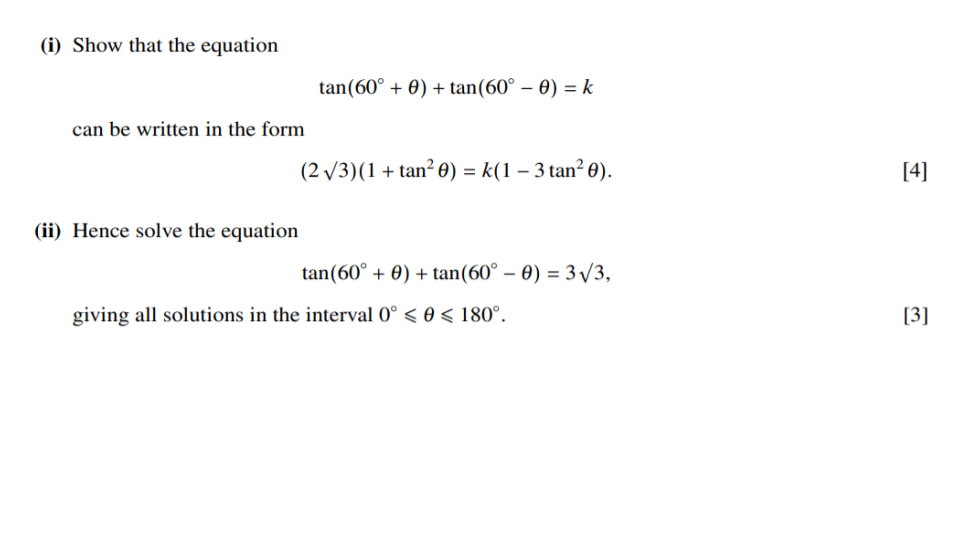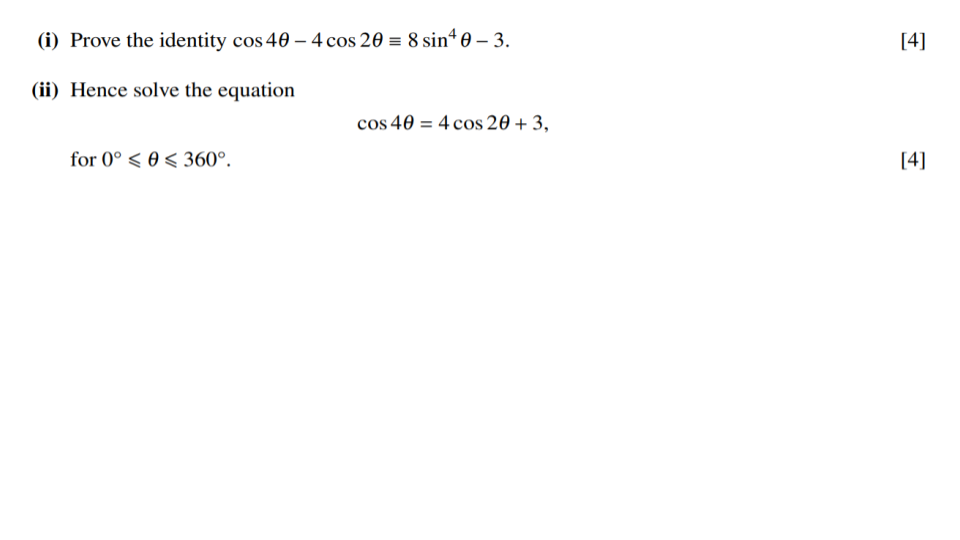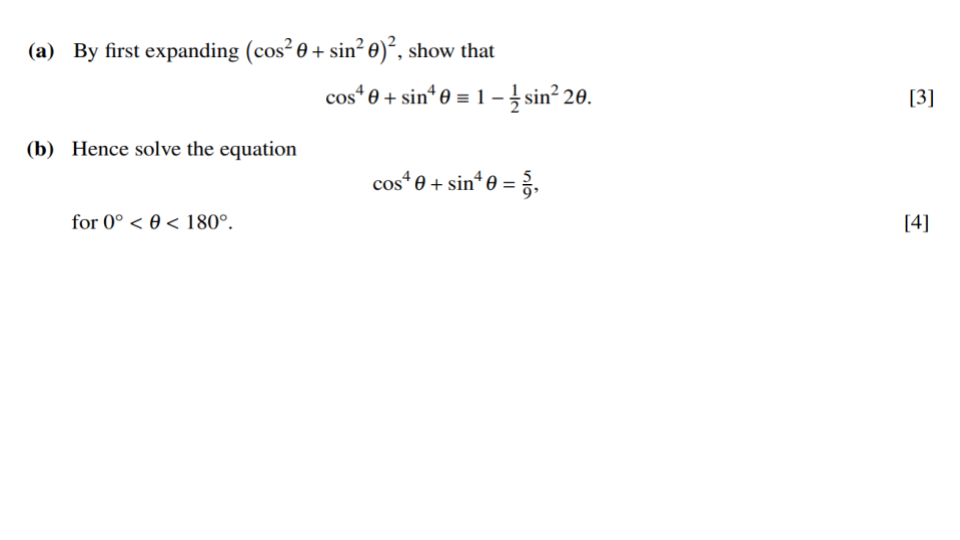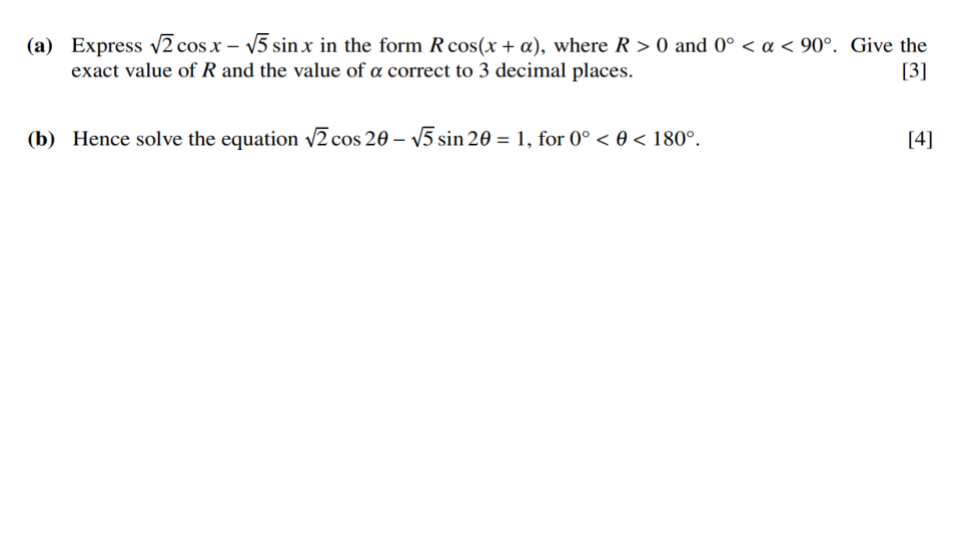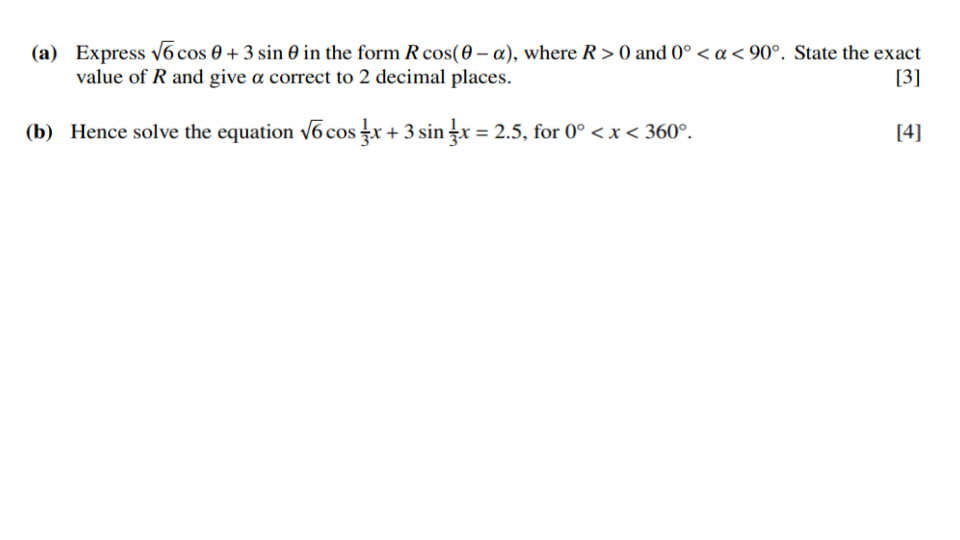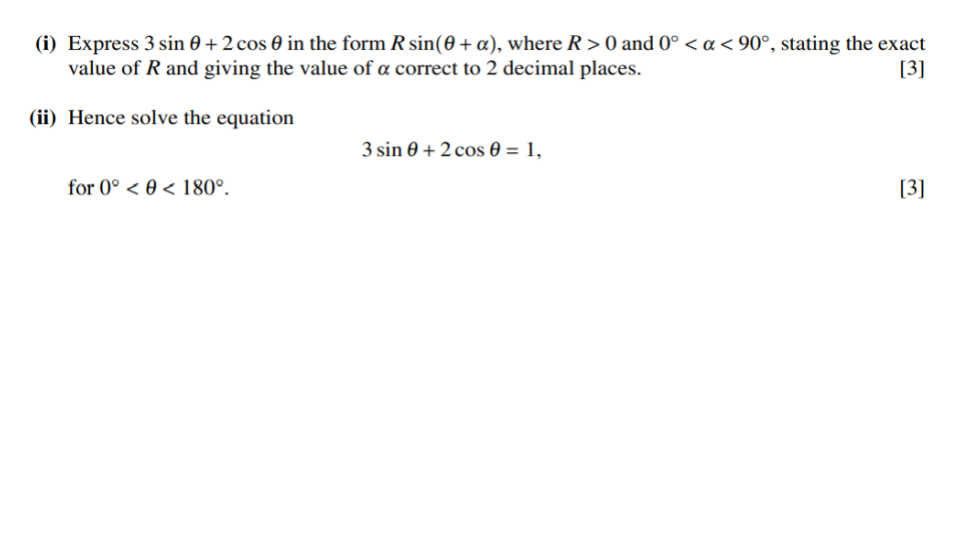Trigonometry: Past Paper Questions for A Level Maths (Cambridge 9709)
Preparing for your Cambridge International A Level Maths exam?
This page is packed with past paper questions on trigonometry to help you master the topic.
Students need to understand the relationship of the secant, cosecant, and cotangent functions to cosine, sine, and tangent, as well as use the properties and graphs of all six trigonometric functions for angles of any magnitude.
Other key skills include applying trigonometric identities to simplify expressions and solve equations, with a focus on identities such as sec²θ ≡ 1 + tan²θ and cosec²θ ≡ 1 + cot²θ.
Students should also be comfortable using the compound angle formulae of sin(A ± B), cos(A ± B), and tan(A ± B), as well as double angle formulae for sin 2θ, cos 2θ, and tan 2θ.
Additionally, mastering harmonic identities, including expressing a sin θ + b cos θ in the forms R sin(θ ± α) and R cos(θ ± α), is essential for success.
Trigonometry Past Paper Questions (9709)
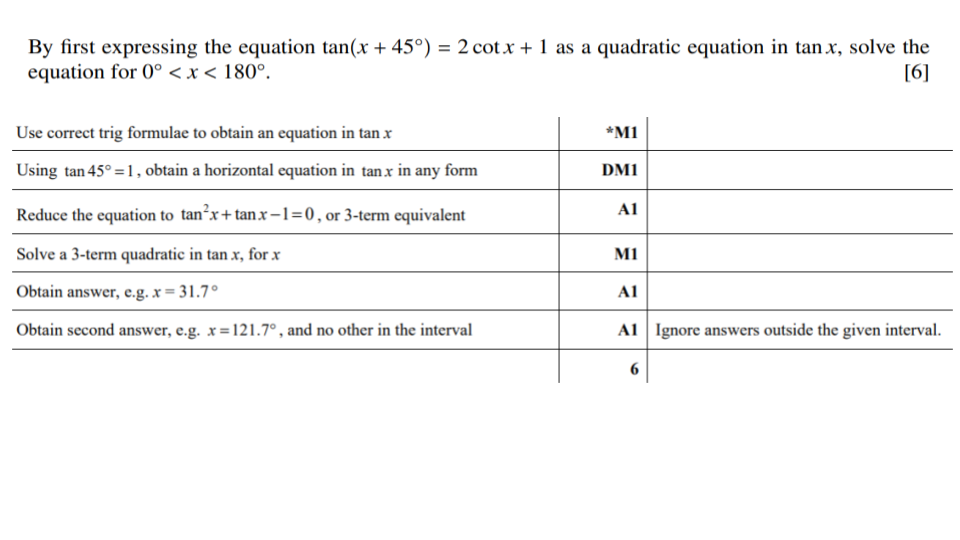
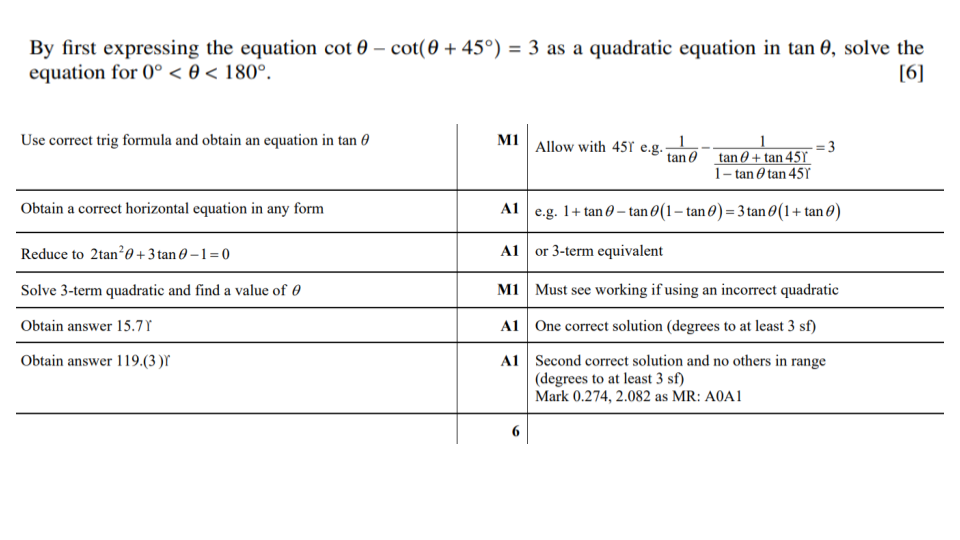
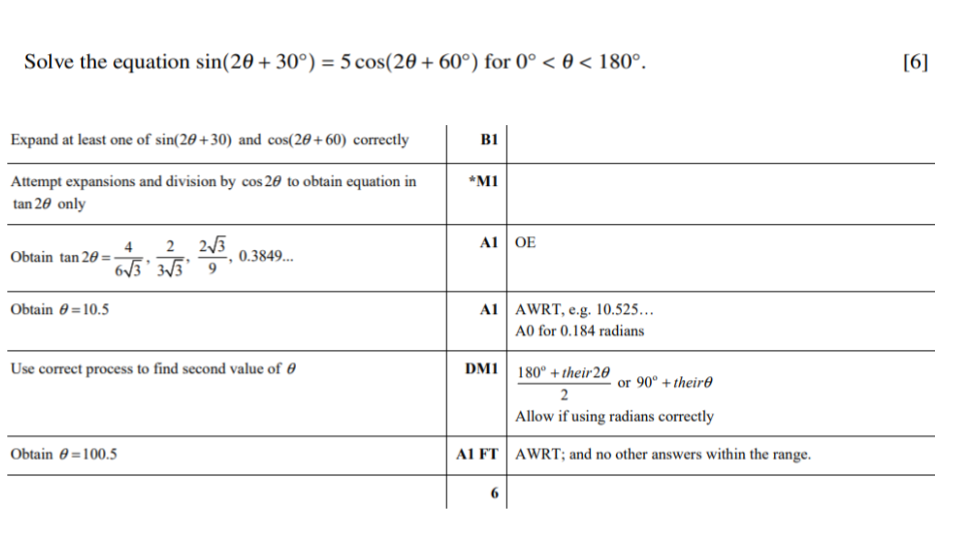
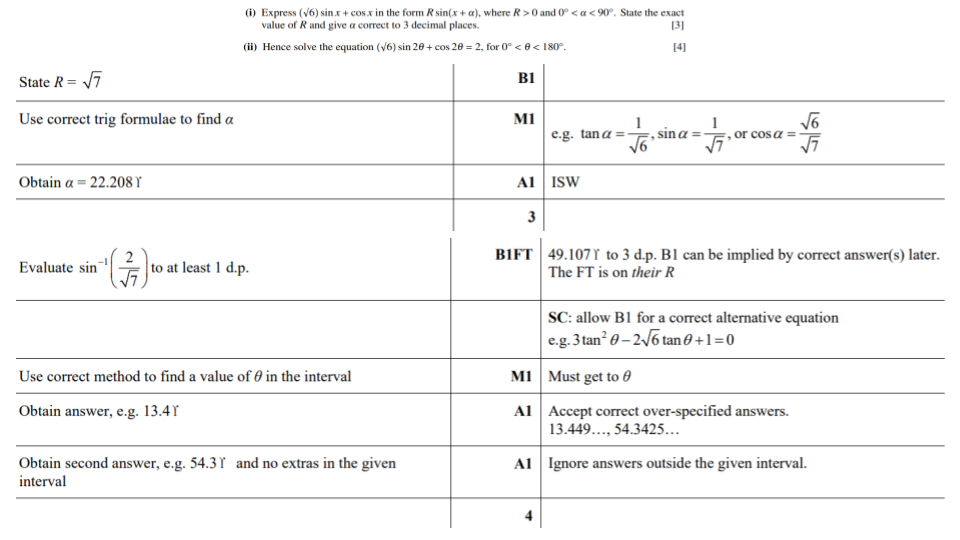
Question 1